Apply Basic Equations to Acquired Data
You can perform basic equations (add, subtract, multiply and divide) with acquired sample spectra. There are a number of reasons why you might want to do this, especially for subtracting a reference spectrum. For more information, see the sections that follow.
To perform any spectral math operation
To perform spectral math, the sample and reference spectra must have the same spectral resolution and be in the same Y-axis unit. If they are not, the software automatically converts the selected reference spectrum to match the selected sample spectrum. In order to subtract, multiply or divide spectra, at least a portion of the spectral range (X-axis) of the two spectra must overlap.
❖ To perform any spectral math operation on a spectrum
-
Acquire or open a spectrum of your sample and make sure that spectrum is selected in the spectral view.
-
Choose Process (menu) > Spectral Math.
The software opens the Spectral Math setup window with the sample spectrum in the left pane and space for a reference spectrum in the right pane.
Spectral Math Setup Window
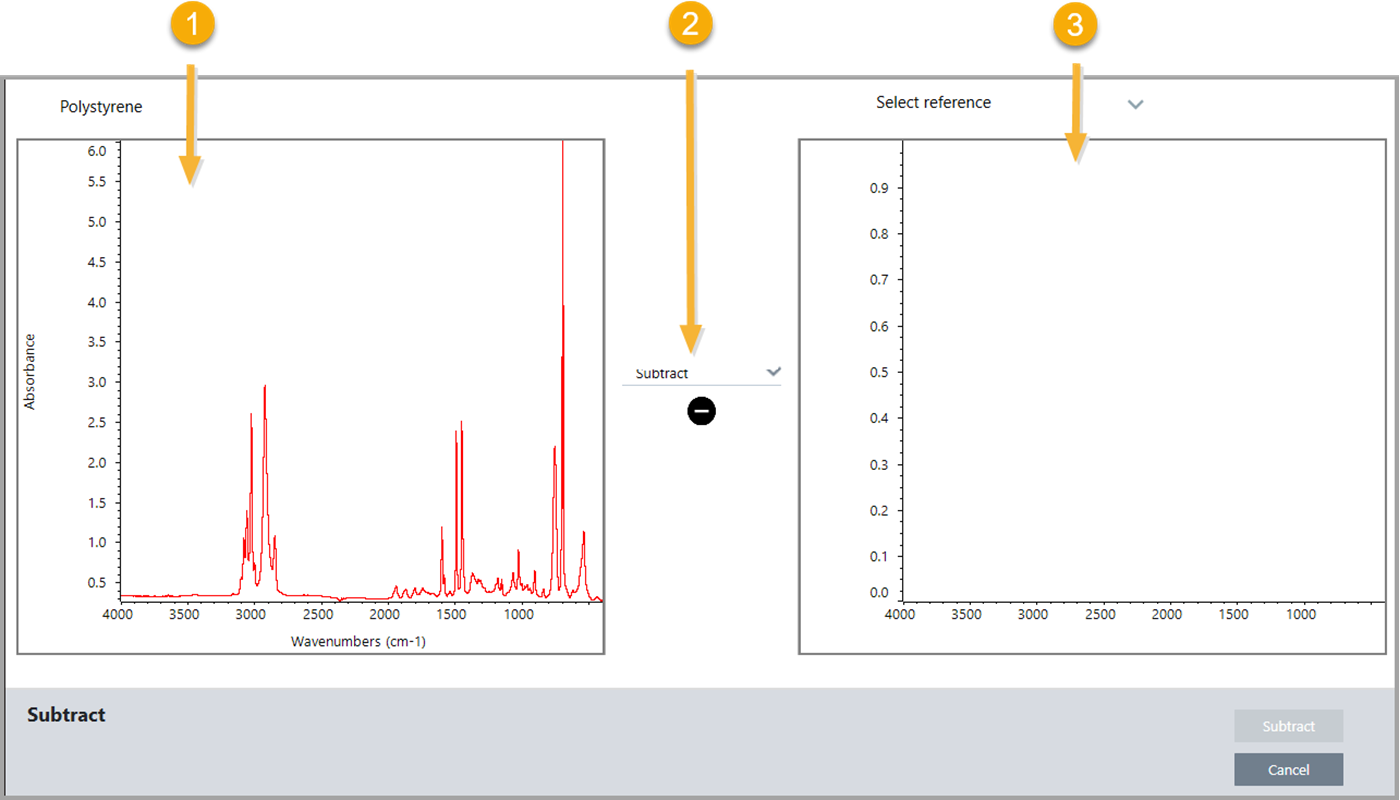
-
Use the settings list between the two panes to select a spectral math operation (Subtract, Add, Multiply or Divide).
-
Use the Select Reference list to search for a spectrum in the current project, another project, or from a spectral library.
-
Click Subtract (Add, Multiply, Divide) to start the operation.
The software opens the Spectral Math operation window with the two original spectra (bottom) and the current result with a factor slide bar (top). Here is an example showing a subtraction result:
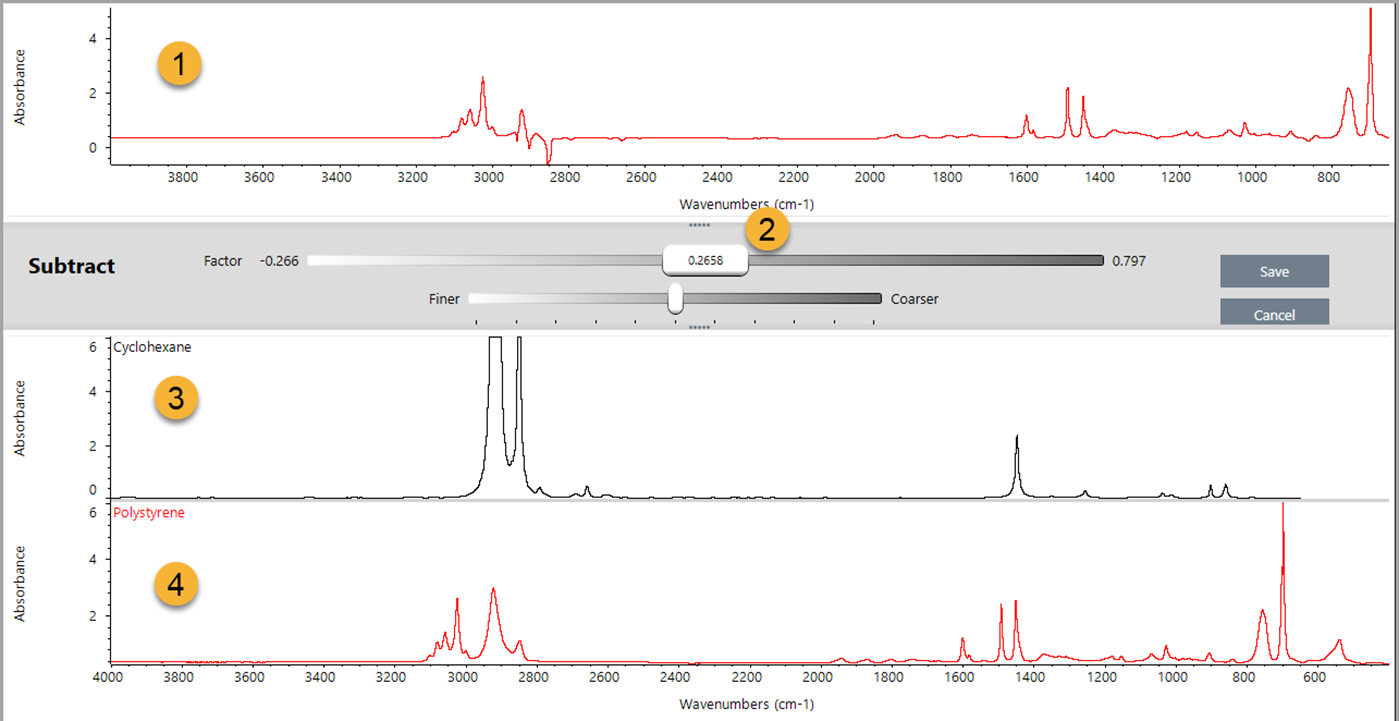
- Current subtraction result
- Factor
- Sample
- Reference
-
Adjust or enter a factor as needed to increase or decrease the intensity of the reference in the result spectrum.
See the sections below for tips on adjusting the factor for each math type.
Use the bottom bar to change the Factor’s adjustable range.
-
Choose Save.
The software shows the spectral view with the subtraction result in the spectral pane and at the top of the results panel, with the original sample and reference spectra directly below it.
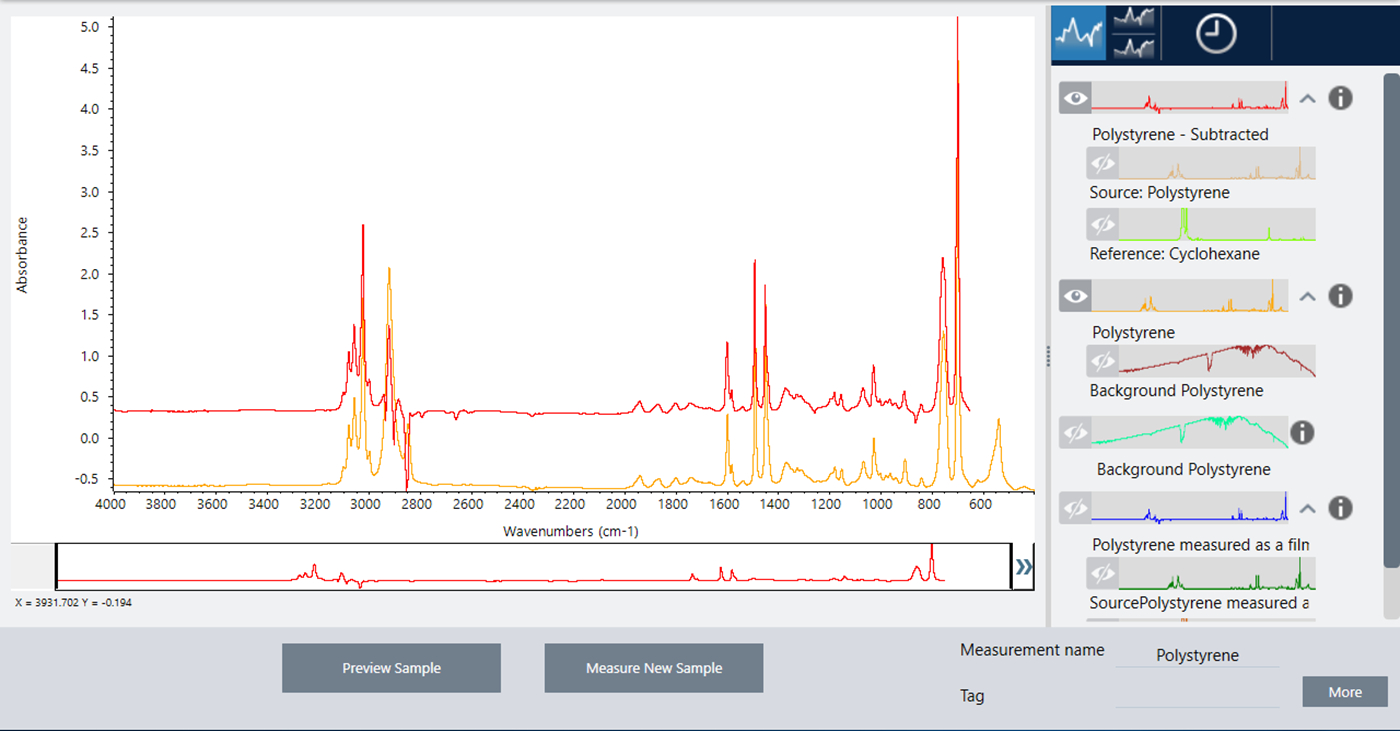
Subtract one spectrum from another (A - B)
Use Subtract to subtract one spectrum from another. Spectral subtraction is useful in a variety of situations. Here are some examples:
- If you measure a sample that is dissolved in a solvent, the spectrum will contain peaks due to the solvent. By subtracting a spectrum of the pure solvent from the sample spectrum, you can eliminate the solvent peaks and produce a “clean” spectrum of the sample material.
- When you measure a sample that is a mixture of two or more components, the spectrum is, theoretically, the sum of the spectra of all the components. By subtracting a spectrum of a pure component from the sample spectrum, you can produce a simpler mixture spectrum with that component removed. You can then search that spectrum against a library to identify the remaining components. (In this case, you might want to try using the Multi-Component Search option instead.)
- If you measure a sample that contains an unknown contaminant, the spectrum will contain peaks due to the contaminant. By subtracting a spectrum of uncontaminated sample material from the first spectrum, you can produce a residual spectrum of the contaminant. You can then search that spectrum against a library to identify the contaminant.
- If you collect spectra to monitor the quality of a material being produced, you can more easily detect changes from one batch to the next by subtracting one sample spectrum from the next (or vice versa) than by just comparing the spectra visually.
Tips on subtracting spectra
- To determine the subtraction factor, watch the changes in the common peaks as you change the factor. The common peaks in the result spectrum should become smaller. The optimum factor is one which produces nulled (or zeroed) common peaks in the subtraction result without subtracting other important spectral information. If you use the correct factor, the peaks present in the result will be due solely to the sample material of interest.
- The initial subtraction factor is automatically calculated from the displayed region. If you display a different spectral region and perform the subtraction again, the difference spectrum will probably be different because the subtraction factor changed.
- When you subtract a reference spectrum from a sample spectrum, the baseline regions are subtracted along with the regions that contain peaks. If the sample spectrum's baseline is not flat and at zero absorbance (or 100% transmittance), the baseline of the subtraction result will have the same undesirable characteristics. If you correct the baseline first, you can obtain a “clean” subtraction in which corresponding peaks are subtracted out, without baseline problems in the result.
- When you subtract the spectrum of a pure reference material from that of a mixture, the peaks may not subtract cleanly. This is because the reference spectrum does not account for any changes that may occur due to molecular interactions with the other components in the mixture or differences in relative concentrations of components. These conditions may cause some peaks to shift slightly or change shape.
Add two spectra together (A + B)
Use Add to add two spectra together. Adding spectra can be useful in the following situations:
-
Add can be used to join together two spectra of different spectral ranges.
-
By adding two pure component spectra together, you can produce a theoretical composite spectrum that is the sum of the two component spectra. This theoretical composite spectrum can be compared with an unknown mixture spectrum in a quantitative analysis.
Tips on adding spectra
- Use the Factor setting to scale the reference spectrum up or down before adding it to the sample spectrum.
- If only one of the spectra contains data points in a spectral region, the Y value of the other spectrum is considered to be zero in that region when the spectra are added.
Multiply one spectrum by another (A * B)
Use Multiply to multiply two spectra. Most people use divide rather than multiply for most applications. But multiplying spectra can be useful for reprocessing a spectrum with a different background. For example, if you measure a sample that is adhered to a matrix, you can acquire a single beam spectrum of just the matrix and use that spectrum to cancel out the original background and replace it with the new one. Here is the equation:
S * B1/B2
Where:
S= sample spectrum (processed with original background)
B1 = original background
B2 = new background
Divide one spectrum by another (A / B)
Use Divide to divide one spectrum by another. Dividing spectra can be useful for reprocessing a spectrum with a different background. For example, if you measure a sample that is adhered to a matrix, you can acquire a single beam spectrum of just the matrix and use that spectrum to cancel out the original background and replace it with the new one. Here is the equation:
S / B1/B2
Where: S= sample spectrum (processed with original background)
B1 = original background
B2 = new background
Tips on dividing spectra
- Data points that have zero absorbance values in the original sample spectrum will produce very strong absorbance values in the resulting spectrum.
Using spectral math with data security
When “Require reason for change for Spectral Math” is enabled in the Thermo Scientific Security Suite, Spectral Math requires a change reason and signature before the results can be saved, and the following change event is recorded in the audit log:
- Date and time
- Operation performed: subtract, add, multiply, divide
- Sample spectrum title
- Reference spectrum title
- Factor

